[논문] Identity Mappings in Deep Residual Networks
본 논문에서는 residual building block들의 propagation formulation을 분석한다. 분석은 identity mapping을 skip connection으로 사용하고 after-addition activation을 쓸 때 forward나 backward signal들은 한 block에서 다른 어떠한 block으로도 직접적으로 전파될 수 있음을 제시한다. 이는 더 쉬운 학습과 일반화를 가진 새로운 residual unit을 설계하는데에 영감을 준다.
1 Introduction
Deep residual networks (ResNets)는 많은 "Residual Unit"이 쌓인 구조를 가진다. 각 unit은 다음과 같이 나타낼 수 있다:
$$\mathbf{y}_l = h(\mathbf{x}_l) + \mathcal{F}(\mathbf{x}_l, \mathcal{W}_l),$$
$$\mathbf{x}_{l+1} = f(\mathbf{y}_l),$$
- $x_l$, $x_{l+1}$: l-th unith의 input과 output
- $\mathcal{F}$: residual function
- $h(x_l)=x_l$: identity mapping
- $f$: ReLU
ResNet은 ImageNet과 MS COCO 같은 데이터셋에서 가장 좋은 성능을 가지고 있다. 그 핵심 아이디어는 "skip connection"을 이용하여 $h(x_l)$에 더해지는 residual function을 학습하는 것이다.
본 논문에서는 deep residual network에서 정보 전달의 "direct" path를 만드는 것을 탐구한다. Residual unit 안에서만의 전파가 아니라 전체 네트워크에서의 shortcut들을 탐구한다.
연구 결과 $h(x_l)$과 $f(y_l)$이 모두 identity mapping이라면 forward path와 backward pass에서 신호가 하나의 unit에서 다른 unit들로 직접적인 전파를 하게 된다는 것을 찾아냈다.
Skip connection들의 역할을 이해하기 위해 다양한 $h(x_l)$들을 비교분석 한다. 실험을 통해 identity mapping이 scaling, gating, 1x1 convolution에 비해 가장 빠른 error reduction과 training loss를 가진다는 것을 발견했다.
Identity mapping을 구성하기 위해서 activation function들을 weight layer들의 "pre-activation" 관점으로 본다.
- 이는 coventional wisdom인 "post-activation"과 상반되는 개념이다.
이 유닛으로 구성된 1001-layer ResNet은 CIRAR-10/100에서 경쟁력있는 결과를 보여준다. 또 이 ResNet은 기본 ResNet보다 더 쉬운 학습과 일반화 성능을 가지고 있다.
2 Analysis of Deep Residual Networks
기존 Residual Unit은 다음과 같은 계산을 거치게 된다:
$$\mathbf{y}_l = h(\mathbf{x}_l) + \mathcal{F}(\mathbf{x}_l, \mathcal{W}_l),$$ -- (1)
$$\mathbf{x}_{l+1} = f(\mathbf{y}_l),$$ -- (2)
- $x_l$, $x_{l+1}$: l-th unith의 input과 output
- $\mathcal{W}_l=\{W_{l,k}|1<=k<=K\}$: l-th Residual Unit에 연관된 weight와 bias들
- K는 Residual Unit 안에 있는 layer 수 (기존은 2 또는 3개)
- $\mathcal{F}$: residual function
- $h(x_l)=x_l$: identity mapping
- $f$: ReLU
위 식에서 만약 $f$ 또한 identity mapping이라면 위 두 식을 합칠 수 있다. ($h(x_{l+1}==y_l$)
$$\mathbf{x}_{l+1} = \mathbf{x}_l + \mathcal{F}(\mathbf{x}_l, \mathcal{W}_l).$$ -- (3)
재귀적으로, $\mathbf{x}{l+2} = \mathbf{x}{l+1} + \mathcal{F}(\mathbf{x}{l+1}, \mathcal{W}{l+1}) = \mathbf{x}_l + \mathcal{F}(\mathbf{x}l, \mathcal{W}l) + \mathcal{F}(\mathbf{x}{l+1}, \mathcal{W}{l+1}), \text{ etc.}$ 이다.
따라서 모든 deeper unit L과 shallow unit l에 대해
$$\mathbf{x}_L = \mathbf{x}l + \sum{i=l}^{L-1} \mathcal{F}(\mathbf{x}_i, \mathcal{W}_i),$$ -- (4)
를 얻을 수 있다.
위 식은 유용한 특성들을 가진다:
- Deeper unit L에 대한 feature $x_L$은 어떤 shallower unit l의 feature $x_l$과 residual function ($ \sum{i=l}^{L-1} \mathcal{F}$)의 합으로 나타낼 수 있다.
- 어느 deep unit L의 feature $x_L$은 $\mathbf{x}_L = \mathbf{x}0 + \sum{i=0}^{L-1} \mathcal{F}(\mathbf{x}_i, \mathcal{W}_i)$ 이다. 이는 "plain network"에서 $x_L$이 matrix-vector products ($\prod_{i=0}^{L-1} W_i \mathbf{x}_0$)인 것과 비교된다.
위 식은 backward propagation에서도 유용한 특성을 가진다. Loss function을 $\mathcal{E}$라고 할 때:
$$\frac{\partial \mathcal{E}}{\partial \mathbf{x}_l} = \frac{\partial \mathcal{E}}{\partial \mathbf{x}_L} \frac{\partial \mathbf{x}_L}{\partial \mathbf{x}_l} = \frac{\partial \mathcal{E}}{\partial \mathbf{x}_L} \left(1 + \frac{\partial}{\partial \mathbf{x}l} \sum{i=l}^{L-1} \mathcal{F}(\mathbf{x}_i, \mathcal{W}_i) \right)$$ -- (5)
- $ \frac{\partial \mathcal{E}}{\partial \mathbf{x}_l} $을 두개의 additive terms로 나눌 수 있다.
- $ \frac{\partial \mathcal{E}}{\partial \mathbf{x}_L} $: 다른 weight layer들과 독립적으로 정보를 직접적으로 전파
- 이 term은 어느 shallower unit l에 대해 정보가 직접적으로 전파되게 보장한다.
- $\frac{\partial \mathcal{E}}{\partial \mathbf{x}_L} \left(\frac{\partial}{\partial \mathbf{x}l} \sum{i=l}^{L-1} \mathcal{F} \right)$: Weight layer들을 통해 전파
- $ \frac{\partial \mathcal{E}}{\partial \mathbf{x}_L} $: 다른 weight layer들과 독립적으로 정보를 직접적으로 전파
Discussions
식 (4)와 (5)는 forward와 backward process에서 모두 signal이 어느 한 unit에서 다른 unit으로 직접적인 전파를 할 수 있다는 것을 제시한다.
식 (4)의 기본에는 두가지 identity mapping이 사용된다:
- Identity skip connection: $h(x_l)=x_l$
- $f$ 또한 identity mapping
이런 직접적인 정보 전파 flow들은 아래 figure들에서 회색 arrow로 표현된다.
3. On the Importance of Identity Skip Connections
간단한 modification을 통해 identity shortcut이 아닌 다른 mapping을 생각해보자: $h(x_l)=\lambda_lx_l$
$$\mathbf{x}_{l+1} = \lambda_l \mathbf{x}_l + \mathcal{F}(\mathbf{x}_l, \mathcal{W}_l),$$ -- (6)
- $\lambda_l$은 바뀌는 scalar 값
똑같이 재귀적으로 표현하면 $\mathbf{x}L = \left(\prod{i=l}^{L-1} \lambda_i\right) \mathbf{x}l + \sum{i=l}^{L-1} \left(\prod_{j=i+1}^{L-1} \lambda_j\right) \mathcal{F}(\mathbf{x}_i, \mathcal{W}_i)$ 이다. 간단히 표현하면:
$$\mathbf{x}L = \left(\prod{i=l}^{L-1} \lambda_i\right) \mathbf{x}l + \sum{i=l}^{L-1} \hat{\mathcal{F}}(\mathbf{x}_i, \mathcal{W}_i),$$ -- (7)
- $\hat{\mathcal{F}}: Scalar들을 residual function들로 흡수해 나타냄
식 (5)와 비슷하게 backpropagation은 다음과 같이 나타내진다:
$$\frac{\partial \mathcal{E}}{\partial \mathbf{x}_l} = \frac{\partial \mathcal{E}}{\partial \mathbf{x}L} \left(\left(\prod{i=l}^{L-1} \lambda_i\right) + \frac{\partial}{\partial \mathbf{x}l} \sum{i=l}^{L-1} \hat{\mathcal{F}}(\mathbf{x}_i, \mathcal{W}_i)\right).$$ --(8)
식 (5)와 다른점은 첫번째 더해지는 term이 $\lambda_i$들의 곱으로 나타내 진다는 점이다.
- 만약 모든 i에 대해 $\lambda_i > 1$라면 이 term은 지수적으로 큰 값을 가진다.
- 반대로 모든 i에 대해 $\lambda_i < 1$라면 지수적으로 작은 값을 가지게 된다.
- 두 경우 모두 backpropagation signal으로 최적화를 하기 어렵게 만든다.
위 분석을 통해 만약 skip connection $h(x_l)$이 복잡한 형태를 가지게 된다면 식 (8)처럼 첫번째 term이 $\prod_{i=l}^{L-1} h'_i$ 형식을 가지게 된다는 것을 알 수 있다. (h'은 h의 미분값)
이는 학습 과정에서 정보 전파를 방해하는 요소이다.
3.1 Experiments on Skip Connections
실험은 기존에 제시된 110-layer ResNet과 CIFAR-10을 사용해 진행한다.
- 54 two-layer Residual Unit (각각 3x3 covolution layer)으로 구성
모든 결과는 각 구조를 CIFAR에 5번 실행한 후 median 값으로 보고한다.
이 섹션에 있는 모든 실험들은 $f=ReLU$를 사용한다. $f$로 identity mapping을 사용하는 실험은 다음 section에서 진행한다.
Variants들과 그 결과는 다음과 같다:

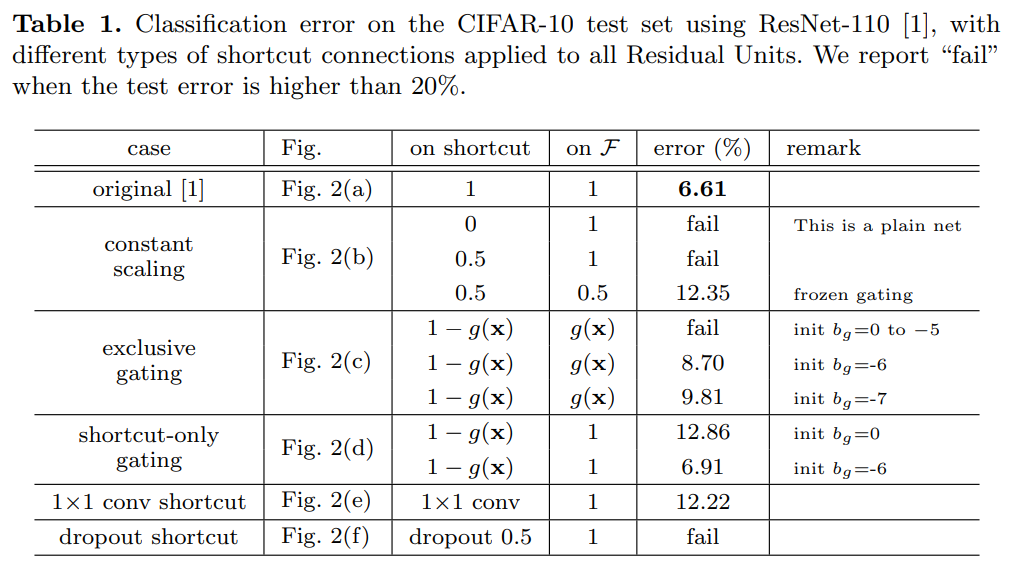
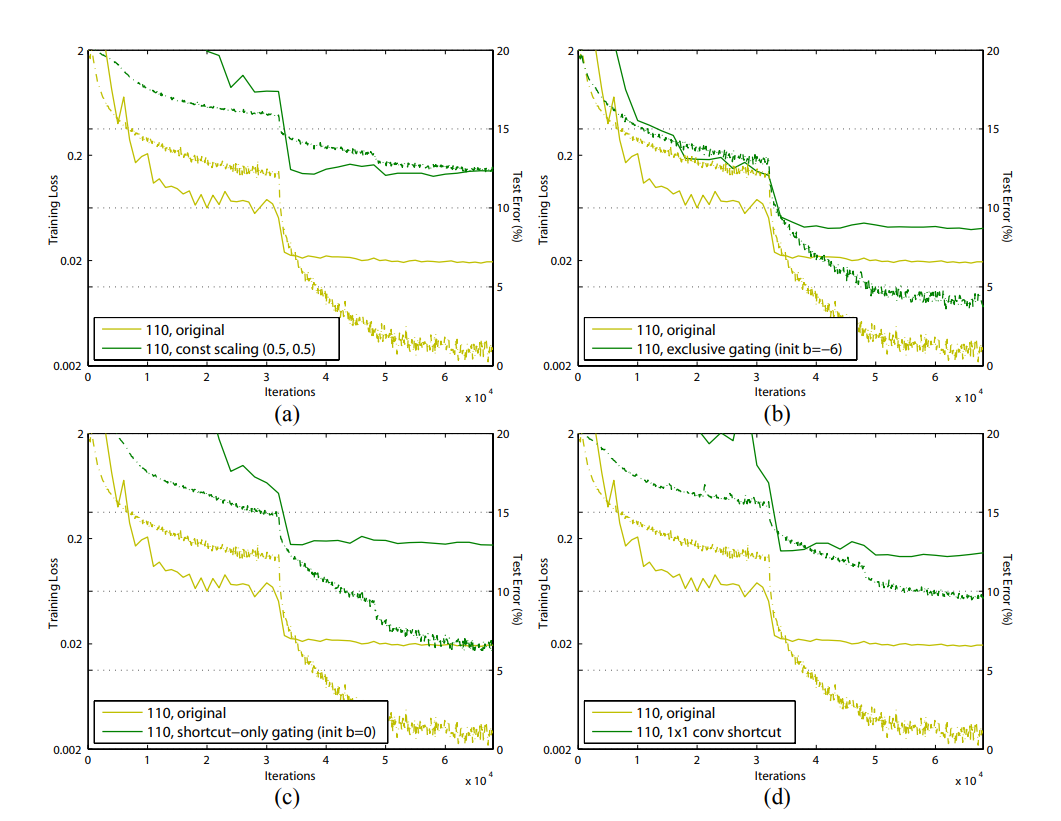
Constant scaling
$\lambda=0.5$로 설정하고 $\mathcal{F}$는 두가지 경우를 연구한다:
- $\mathcal{F}$는 scale 하지 않는다
- $\mathcal{F}$ 또한 0.5로 scale 한다
전자의 경우는 수렴하지 않는다. 후자의 경우 수렴하지만 test error가 baseline ResNet보다 더 높다.
따라서 scale down shortcut signal은 최적화를 더 어렵게 한다는 것을 알 수 있다.
Exclusive gating
Highway Networks의 gating 기법의 gating function $g(\mathbf{x}) = \sigma(W_g \mathbf{x} + b_g)$를 적용한다.
- $\sigma(x)=\frac{1}{1+e^{-x}}$: sigmoid 함수
Convolutional network에서 g(x)는 1x1 convolution layer를 통해 실현된다.
이 gating function은 element-wise multiplication으로 신호를 변경한다.
Exclusive gate를 먼저 탐구한다. $\mathcal{F}$ path는 g(x)로 scale 되고 shortcut path는 1-g(x)로 scale 된다.
Figure 2(c)를 보면 알 수 있듯이 bias $b_g$의 초기값이 수렴에 큰 영향을 주는 것을 알 수 있다.
실험에서 $b_g$의 값을 0부터 -10까지 1씩 줄여가며 hyper-parameter search를 진행했다.
가장 좋은 성능을 내는 값은 8.70%로 여전히 baseline 모델인 ResNet-110보다 낮은 성능을 보인다.
Exclusive gating 기법의 영향은 두가지로 분류된다.
- 1-g(x)가 1에 가까워질 때 gated shortcut은 identity에 가까워지고 정보 전파를 돕는다.
- 하지만 이 경우 g(x)가 0에 가까워져 함수 $\mathcal{F}$를 막게된다.
Shortcut-only gating
위 경우와 다르게 function $\mathcal{F}$는 scale 하지 않는다. Shortcut path는 마찬가지로 1-g(x)로 scale 한다.
이 경우에서 $b_g$의 초기값이 매우 중요하다. (Table 1 참고)
- $b_g$ 값이 0일 때 -> 초기 1-g(x) 값이 0.5 -> 낮은 수렴 값 (12.86%)
- $b_g$ 값이 -6일 때 -> 초기 1-g(x) 값이 1에 가까움 -> baseline ResNet-110과 비슷한 수렴 값 (6.91%)
1x1 convolutional shortcut
다음 실험에서는 identity 대신 1x1 convolutional chortcut connection을 사용한다.
23-layer ResNet에서는 이 경우가 더 좋은 성능을 낼 수 있었다. 하지만 110-layer ResNet에서는 오히려 낮은 결과를 보인다.
이는 Residual Unit들이 너무 많이 쌓이면 가장 짧은 path도 signal propagation을 방해한다는 것을 보여준다.
Dropout shortcut
Dropout=0.5를 이용한 실험에서는 network가 수렴하지 않는다. Dropout은 scale $\lambda$ 0.5를 적용시키는 것과 같은 역할을 수행하고 0.5를 사용한 constant scaling처럼 signal propagation을 방해한다.
3.2 Discussion
Figure 2의 회색 화살표로 나타나 있듯이 shortcut connection들이 정보 전파에 가장 직접적인 path 들이다.
이 path에 multiplicative 조절들은 (scaling, gating, 1x1 convolution, dropout) 정보 전파를 방해하고 최적화 문제를 만들 수 있다.
1x1 convolutional shortcut들은 더 많은 parameter를 사용하기 때문에 더 강한 representational 능력이 있어야 한다.
사실 shortcut-only gating과 1x1 covolution은 같은 solution space를 가진다.
그럼에도 불구하고 더 높은 training error 가진다는 것은 모델들이 representational 능력의 부족이 아닌 최적화 문제를 가지고 있다는 것을 알 수 있다.
4 On the Usage of Activation Functions
위 섹션 실험들은 identity mapping을 사용하는 activation $f$인 식(5)와 식(8)에 힘을 실어준다.
위 실험들에서는 f로 ReLU를 사용하는데 이번 섹션에서는 이 f의 영향을 탐구해본다.
f를 identity mapping으로 바꾸기 위해 activation function들을 재배치 한다.

4.1 Experiments on Activation
이 섹션에서는 ResNet-110과 164-layer Bottleneck 구조 (ResNet-164)를 사용해 실험을 진행한다.
- Bottleneck 구조는 1x1, 3x3, 1x1 layer로 구성되어 있고 기존 two-3x3 Residual Unit과 비슷한 계산 복잡도를 가진다.
ResNet-164는 CIFAR-10에서 5.93%로 경쟁력 있는 결과를 보여준다.
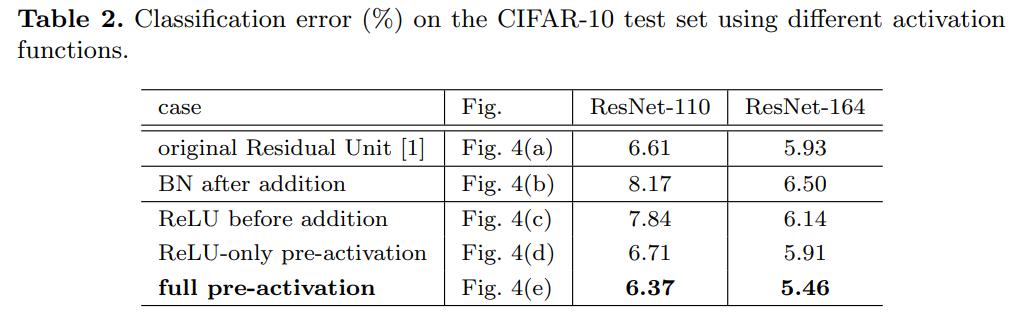

BN after addition
f를 identity mapping으로 바꾸기 전에 반대로 BN을 덧셈 후 적용해본다.
이 경우에 f는 BN과 ReLU를 거치게 된다.
결과는 Table 2에서 확인할 수 있듯이 baseline보다 더 못한 성능을 가진다.
기존 design과 다르게 BN layer는 shortcut을 지나가는 신호를 바꾸게 되고 이는 정보 전파를 방해한다.
ReLU before addition
가장 간단하게 f를 identity mapping을 ㅗ바꾸는 방법은 ReLU를 addition 전으로 옮기는 것이다.
하지만 이는 transform $\mathcal{F}$가 non-negative 값을 가지게 한다. (이상적인 residual function은 $(-\inf, +\inf)$의 값을 가진다)
따라서 forward 전파 신호는 monotonically increase 하게 된다. 이는 모델의 표현력을 낮추게 되고 더 낮은 성능을 가지게 한다.
Post-activation or pre-activation?
기존 구조에서는 activation f가 Residual Unit의 두가지 path에 모두 영향을 준다: $\mathbf{y}_{l+1} = f(\mathbf{y}_l) + \mathcal{F}(f(\mathbf{y}l), \mathcal{W}{l+1})$
본 논문에서는 activation $\hat{f}$가 오직 $\mathcal{F}$의 apth만 영향을 주도록 설계한다: $\mathbf{y}_{l+1} = \mathbf{y}_l + \mathcal{F}(\hat{f}(\mathbf{y}l), \mathcal{W}{l+1})$
정리하면:
$$\mathbf{x}_{l+1} = \mathbf{x}_l + \mathcal{F}(\hat{f}(\mathbf{x}_l), \mathcal{W}_l)$$ -- (9)
식(9)는 식(4)와 매우 유사하고 backward formulation 또한 식(5)의 형태를 가진다.
식(9)에서는 after-addition activation이 identity mapping이 된다.
이 설계는 만약 이 새로운 after-addition activation $\hat{f}$가 비대칭적으로 적용됐다면 이는 다음 Residual Unit에 pre-activation을 $\hat{f}$로 recasting 하는 것과 같다는 의미를 가진다. (Figure 5를 참고)
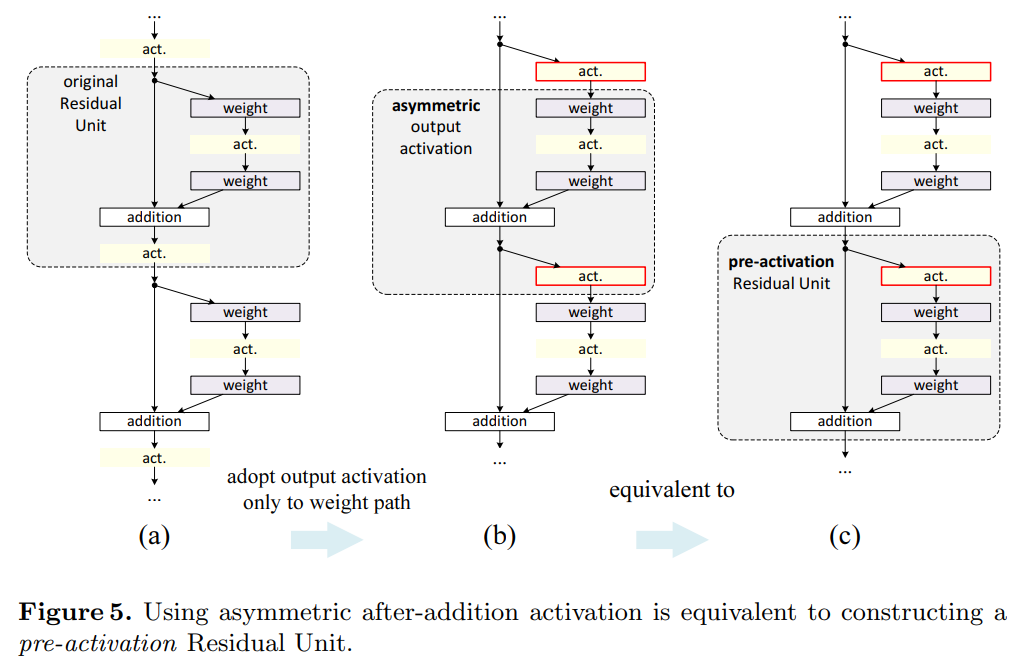
Post-activation과 pre-activation의 차이는 element-wise addition의 유무이다.
N개의 layer가 있는 plain network에서는 N-1개의 activation을 가지고 pre-나 post-activation을 구분할 필요가 없다.
하지만 branch layer에서는 위치가 중요해진다.
실험에서는 두가지 구조를 비교한다:
- ReLU-only pre-activation
- full pre-activation (ReLU + BN)
Table 2에 따르면 ReLU-only pre-activation은 기존 baseline 모델과 매우 유사한 정확도를 보여준다. 이는 ReLU layer가 BN과 함께 쓰지이 않았기 때문에 BN layer의 혜택을 얻지 못하기 때문으로 추측된다.
반대로 BN과 ReLU가 모두 pre-activation에 사용됐을 때 유의미한 크기의 성능 향상을 얻을 수 있었다.

Table 3에서 알 수 있듯이 다양한 ResNet 구조에서 모두 향상된 결과를 보여준다.
- ResNet-110 (1 layer skip): Residual Unit이 layer 1개로 구성됨)
4.2 Analysis
Pre-activation의 영향은 두가지로 분류된다. 첫번째는 최적화가 더 쉬워진 이유이다. 두번째는 BN을 pre-activation으로 사용하는 것이 모델의 일반화 성능을 향상시켰기 때문이다.
Ease of optimization
이 영향은 1001-layer ResNet을 학습할 때 가장 명확하게 드러난다.
- 기존 디자인에서는 학습 초기에 training error가 매우 느리게 감소한다.
- f = ReLU인 경우 signal이 음수 값이라면 영향을 받고 많은 Residual Unit을 통과하면서 그 영향이 커지고 좋은 approximation을 가지지 못한다.
- 반면에 f 가 identity mapping인 경우 training loss가 매우 빠르게 감소한다 (Figure 1)
- f가 identity mapping인 경우 signal이 두 unit 사이에 간섭 없이 직접적으로 전파되기 때문이다.
또한 f = ReLU가 적은 수의 layer를 가지는 ResNet에는 큰 영향을 주지 않는 것을 발견했다.
- Response 관찰 결과 약간의 학습이 이루어진 이후 식 (1)에 있는 $y_l$가 대부분 0보다 크도록 weights가 조정됨을 알아냈다.
- 하지만 0이하 값을 잘라내는 truncation은 1000 layer 모델에서 훨씬 더 자주 발생한다.
Reducing overfitting
Pre-activation unit의 두번째 제시된 효과는 regularization (일반화)이다.
- Figure 6 오른쪽 그림을 보면 비록 pre-activation 버전이 더 높은 training loss로 수렴하더라도 더 낮은 test error를 가진다
- 이는 ResNet-110 (1-layer), ResNet-164에서 CIFAR-10, 100을 사용했을 때 똑같이 관찰된다.
- 기존 Residual Unit은 BN이 signal을 정규화하더라도 shortcut에 더해지고 합쳐진 signal은 정규화되어있지 않다.
- 반대로 pre-activation 버전에서는 모든 weight layer로 들어가는 input은 정규화되어있다.
5 Results
Comparisons on CIFAR-10 / 100

Table 4는 CIFAR-10/100에 대한 state-of-the art 기법들을 비교한다. 본 논문에서 제시된 모델들도 경쟁령있는 정확도를 보여준다.
위 결과들에는 network width나 filter 크기들을 조절하지 않았고 dropout 또한 사용하지 않았다. 이 결과들은 단순히 모델의 depth를 증가시켜 얻은 결과이다.
Comparisons on ImageNet
1000-class ImageNet 데이터셋에 대한 결과도 보고한다.
Figure 2와 3에서 사용된 skip connection을 Resnet-101에 적용시켰을 때 똑같은 최적화 문제를 발견했다.
- Non-identity shorcut들을 비교했을 때 기존 ResNet보다 훨씬 더 높은 training error를 확인했고 더 학습을 진행하지 않았다
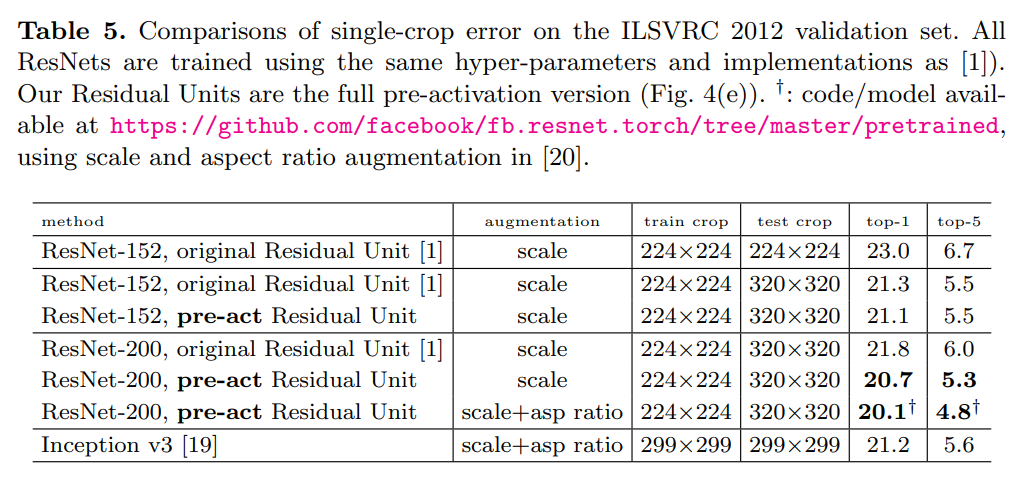
Table 5는 ResNet-152와 ResNet-200의 결과를 보여준다.
- ResNet-152에서는 original과 pre-activation 모델 간 큰 성능 차이를 얻지 못했다
- 하지만 overfitting 문제를 가지는 ResNet-200에서는 pre-activation 버전이 1.1% 더 좋은 성능을 보여준다
Computational Cost
본 논문에서 제시된 모델들의 계산 복잡도는 depth에 linear한 관계를 가진다.
CIFAR에서는 ResNet-1001을 GPU 2개에 학습하는데 27시간이 걸린다. ImageNet에서 ResNet-200을 8개의 GPU를 사용해 학습하는데에 3주가 걸린다.
6 Conclusions
본 논문에서는 deep residual network들의 connection 기법 뒤에 숨겨진 propagation formulation들을 연구한다.
본 연구에서는 identity shortcut connection과 after-addition activation이 정보 전파를 부드럽게 하는데에 중요한 역할을 한다 보여준다.
