100개가 넘는 layer를 가진 convolutional network들은 여러 benchmark들에서 경쟁력있는 결과를 보여준다. 하지만 이런 deep network들을 학습스키는데 많은 도전점들이 있다. 기울기나 forward flow가 사라지기도 하고 학습 시간이 매우 오래 걸린다.
본 논문에서는 stochastic depth 기법을 제시한다. 이 기법은 짧은 network들을 학습시키고 test 시에는 deep networ들을 사용한다. 학습은 깊은 network로 시작해 각 mini-batch마다 무작위로 subset layer들을 identity function을 이용해 우회한다. 이 기법을 통해 학습 시간을 줄이고 정확도를 올릴 수 있다.
1. Introduction
Network의 깊이는 모델의 표현력에 주요한 결정요소이다. 하지만 깊은 network들은 다음과 같은 문제를 가진다:
- Backward propagation에서 vanishing gradient
- 연속적인 multiplication 또는 convolution
- Forward propagation에서 diminishing feature reuse
- 마찬가지로 연속적인 multiplication 또는 convolution에 의한 정보 손실
- 최근 Identity mapping을 통한 직접적인 정보 전달로 성능 향상 연구 진행
- 긴 학습 시간
- 152-layer ResNet의 경우 2주 소요
본 논문에서는 deep networks with stochastic depth를 제시한다.
- 먼저 deep Residual Network 구조를 만든다
- 그 후 각 mini-batch를 학습할 때 모델의 상당한 부분을 무작위로 없앤다
- 따라서 학습 과정에서는 작은 expected depth를 가지게되지만 test 과정에서는 깊은 depth를 가진다
이 기법으로 학습 시간 뿐 아니라 test error도 현저히 줄일 수 있다.
- 짧은 학습 시간은 짧은 forward와 backward propagation step 크기 때문
- 줄어든 test error는 두가지 이유로 분석:
- 짧은 depth가 backward propagation에서 강화된 기울기 전파 능력을 야기함
- Stochastic depth로 학습된 모델은 다른 depth를 가지는 모델의 ensemble network처럼 작동함
또한 stochastic depth 기법은 모델 정규화에 도움이 되는 것으로 관측된다.
2. Background
Deep network들을 효과적으로 학습시키기 위해 많은 연구가 이루어졌다.
- Bactch Normalization: Hidden layer를 각 mini-batch에 대해 정규화
- Vanishing gradients 문제를 해결하고 강한 정규화 효과
- Highway Networks
- 이전 정보를 변화 없이 다음 layer로 전달하는 "information highways"를 사용
- Residual networks (ResNets)
- Identity mapping을 통해 이전 layer의 정보를 그대로 전파

- Dropout
- 각각의 hidden activation을 독립적인 Bernoulli random variable에 곱함
- "coadaptation" 문제를 줄임
- 수많은 작은 network를 ensemble하는 효과
- 각각의 hidden activation을 독립적인 Bernoulli random variable에 곱함
Dropout과 비슷하게 stochastic depth는 서로 다른 depth를 가지는 network들을 emsemble하는 것과 비슷하다.
Dropout과 다른 것은 network를 thinner하게 만드는 것이 아니라 shorter하게 만든다는 것이다.
Dropout은 Batch Normalization과 함께 쓰이면 그 효과가 없어지고 이는 110-layer ResNet을 통해 보여준다.
실험을 통해 stochastic depth는 Batch Normalization이 사용된 ResNet에서도 효과적이라는 것을 보여준다.
3 Deep Networks with Stochastic Depth
Stochastic depth 학습은 매우 간단한 intuition을 따른다: 학습 과정에서의 neural network effective length를 줄이자.
따라서 ResNet에서 사용되는 것과 비슷하게 skip connection을 사용한다. 하지만 연결 패턴은 각 mini-batch마다 무작위로 바뀐다.
- 각 mini-batch마다 무작위로 layer들을 선택해 transformation function을 없애고 identity skip connection만 유지한다.
ResNet architecture
위 figure 1에 설명된 것처럼 L개의 residual block들을 사용한다. (ImageNet을 제외한 모든 실험은 같은 구조인 network로 진행한다)
Stochastic depth
학습 과정에서 Bernoulli random variable을 이용해 전체 ResBlock을 skip connection으로 우회할지 선택한다.
- bl∈{0,1}: 0 inactive, 1 active
- pl=Pr(bl=1): Active 일 확률
만약 bl=1이라면
- Hl=ReLU(blfl(Hl−1)+id(Hl−1)
bl=0이라면
- Hl=id(Hl−1)
이는 input Hl−1이 항상 양수인 사실을 이용한다.
The survival probabilities
pl은 제시된 모델에서의 새로운 hyperparameter이다. 이를 설정하는 방법은 두가지가 있다:
- 모든 layer에 대해 pl=pL로 설정한다
- Linear decay를 사용한다
- pl=1−lL(1−pL)

Linear decay는 이전 layer들의 feature들이 더 신뢰성이 있고 뒤 layer들에 크게 기여할 것이라는 직관에 기반한다.
뒤 Section 4에서 더 자세한 결과를 비교한다.
Expected network depth
Stochastic depth에서 effective한 ResBlock의 수의 기대값은 다음과 같이 구할 수 있다:
- E(\tildaL)=∑Ll=1pl
위 제시된 linear decay rule을 따르면 기대값은 대략 3L/4 정도이다.
- 110-layer ResNet은 L=54이고 기대값은 40정도이다.
이런 깊이 감소가 vanishing gradient와 정보 손실 문제를 해결하는데에 큰 영향을 준다. (자세한 결과는 section 5에 서술한다)
Training time savings
만약 ResBlock이 특정 iteration에 생략됐다면 forward-backward 계산이나 기울기를 업데이트 할 필요가 없다.
- 대부분의 학습 시간이 forward-backward 계산에 소모되기 때문에 위 linear decay rule을 사용하면 약 25%의 학습 시간을 단축할 수 있다
- 자세한 결과는 뒤 section에서 다룬다
Implicit model ensemble
동일한 깊이를 사용하는 ResNet과 비교해 제시된 기법을 사용하는 모델들은 더 낮은 test error를 보여준다.
이는 implicit한 모델 ensemble의 효과로 해석된다
- L개의 layer가 active 하거나 inactive 할 수 있기 때문에 총 2L개의 network 구성이 가능하다.
- 각 mini-batch당 하나의 network를 선택하게 되고 testing에서는 전체 network의 평균을 사용한다.
Stochastic depth during testing
Test 과정에서 해당 layer의 fl이 활성화 될 확률 pl에 따라 output을 조절한다
HTestl=ReLU(plfl(HTestl−1;Wl)+HTestl−1)
모델 ensemble 관점에서는 모든 가능한 network를 survival probability로 weight해 더한다 해석될 수 있다.
4 Results
본 논문에서는 stochastic depth의 효과성을 다음 dataset들에서 증명한다:
- CIFAR-10, CIFAR-100, SVH, ImageNet
Implementation details
모든 데이터셋에 대해 기존 일정한 depth를 가지는 ResNet과 제시된 stochastic depth를 사용한 ResNet을 비교한다.
- pl 값은 linear decay를 사용하고 p0=1,pL=0.5를 사용한다
- 가장 낮은 validation eorror를 가진 epoch로 test error를 보고한다
- CIFAR-100의 경우 기존 ResNet 논문에서 제시한 110-layer ResNet을 사용한다
- CIFAR-10의 경우에도 같다 (마지막 softmax output 만 다름)
- 각 모델은 filter 수와 feature map 크기가 다른 세가지 종류의 residual block을 사용한다
- 각 종류 그룹 당 18개 residual block
- 각 그룹의 filter size는 16, 32, 64개
- Output dimension이 더 큰 경우 average pooling과 zero padding을 사용해 차원을 맞춘다
CIFAR-10
CIFAR-10
- 32x32 color 이미지
- Training 45000, validation 5000, test 10000
- 증강: Horizontal flippping, translation by 4 pixels
Baseline ResNet & Stochastic depth ResNet
- SGD 500 epochs, mini-batch 128
- Learning rate는 0.1부터 250과 375 epoch마다 10배로 줄임
- Weight decay: 1e-4, momentum 0.9


Table 1에 따르면 stochastic depth로 학습된 모델이 더 높은 test 정확도를 보여준다.
Figure 3에 따르면 stochastic depth로 학습된 모델이 더 높은 fluctuation을 보이지만 더 낮은 test error를 가지는 것을 보여준다.
CIFAR-100
CIFAR-100
- CIFAR-10에서 이미지 종류만 100으로 증가
ResNet 셋업
- CIFAR-10과 완전 동일
마찬가지로 stochastic depth로 학습된 모델이 더 낮은 test error를 보여준다.
SVHN
Street View House Number (SVHM)
- 32x32 color 이미지
- Traning 73257, test 26032
- 추가 학습 샘플 531131개
- Traning에서 400개, 추가 샘플에서 200개를 뽑아 총 6000개의 validation 생성
- 증강은 하지 않음
- 평균과 표준편차를 빼 preprocess 진행
모델 셋업
- Batch size 128, 매 200 iteration마다 vadlidation error 계산
- 152 layer
- Learning rate 0.1로 50 epoch 학습 후 매 30과 35 epoch마다 10으로 나눔

기존 모델의 경우 1.8% test error 후 overfitting이 진행한다.
Stochastic depth로 학습된 모델의 경우 1.75% test error를 보여준다.
Training time comparison

Stochastic depth 기법이 약 25% 더 빠른 학습을 보여준다.
Training with a 1202-layer ResNet
기존 ResNet 논문에서는 CIFAR-10을 1202 layer ResNet으로 학습시키는 시도를 한다. 그 결과 overfitting으로 110-ResNet보다 더 높은 test error인 7.93%를 보여준다.
제시된 stochastic depth 기법을 사용해 같은 1202-layer network를 학습시킨다.
- 300 epoch동안 learning rate 0.01로 "warm-up"
- Learning rate를 0.1로 설정하고 150와 225 epoch에 10으로 나눔

결과는 Figure 4 오른쪽 그림과 Figure 5에 보여진다.
Stochastic depth를 사용한 모델에서 deep ResNet들이 훨씬 더 좋은 성능을 보인다.
ImageNet
ImageNet
- 1000종류 이미지
- Training 50000, testing 100000
ResNet 논문에 따라 50 bottlenect residual block을 사용한 152-layer ResNet을 구성한다.
- Batch size 128, 90 epoch
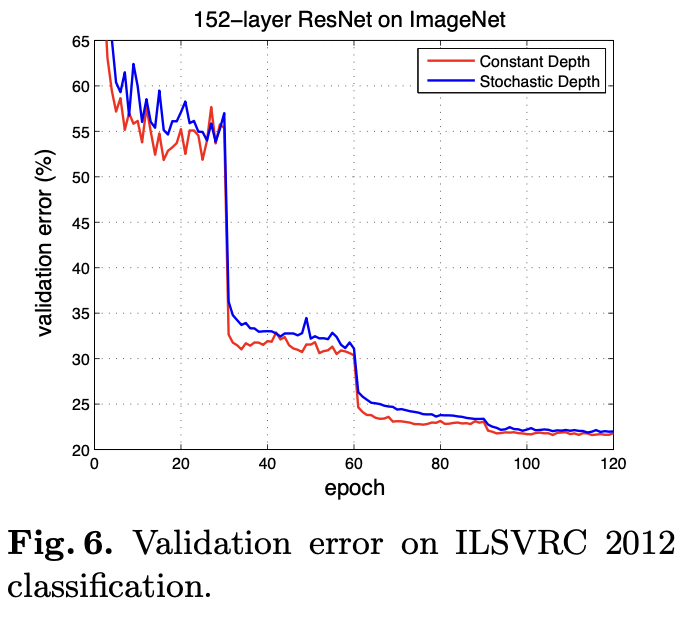
- 기존 모델
- Epoch 90: 23.06%
- Epoch 120: 21.78%
- Stochastic depth
- Epoch 90: 23.38%
- Epoch 120: 21.98%
ImageNet은 CIFAR 데이터셋에 비해 더 복잡하고 때문에 더 큰 모델을 필요로 할 수 있다.
5 Analytic Experiments
Imporved gradient strength

Figure 7는 첫번쨰 convolution layer의 첫번째 ResBlock 기울기의 크기를 비교한다.
- Dotted-line은 learning rate division을 의미
- Stochastic depth 기법이 사용된 모델에서 항상 gradient 크기가 더 큼
- 이는 vanishing gradient 문제를 잘 해결함을 보여줌
Hyper-parameter sensitivity
제시된 기법의 hyperparameter는 survival probability인 pL이다.

Figure 8은 CIFAR-10에 서로 다른 pL 값과 network 깊이에 대한 110-layer ResNet의 정확도를 보여준다.
- 적절한 pL값으로 설정되면 항상 baseline보다 높은 정확도를 보여줌
- Linear decay rule이 uniform rule보다 항상 좋은 성능을 보여줌
이는 stochastic depth가 정확도를 크게 희생시키지 않고 모델 학습을 빠르게 할 수 있음을 보여준다.
Figure 8 오른쪽 그림은 stochastic depth로 기존 baseline 모델을 능가하기 위해서는 "충분한 깊이"가 필요하다는 것을 보여준다.
6 Conclusion
본 논문에서는 매우 깊은 neural network들을 효과적이고 효율적으로 학습하는 기법인 stochastic depth를 제시한다.
'논문 > Computer Vision' 카테고리의 다른 글
| [논문] An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale (2021) (0) | 2025.02.13 |
|---|---|
| [논문] Densely Connected Convolutional Networks (1) | 2025.02.08 |
| [논문] FractalNet: Ultra-Deep Neural Networks without Residuals (2) | 2025.02.07 |
| [논문] Identity Mappings in Deep Residual Networks (0) | 2025.01.18 |
| [논문] Deep Residual Learning for Image Recognition (1) | 2025.01.18 |



